Nonogram
A nonogram (also known as a picture cross) is a grid of squares with a list of numbers along a horizontal and vertical axes. The object of the puzzle is to fill in squares to reveal an image.
The numbers on the axes each dictate a group of squares that need to be filled in. For example, if a row has the numbers “2 3 1”, then that row has a group of 2 consecutive squares filled, followed by 1 or more empty squares followed by 3 squares filled, followed by 1 or more empty squares followed by 1 filled square. There could be empty squares on either end.
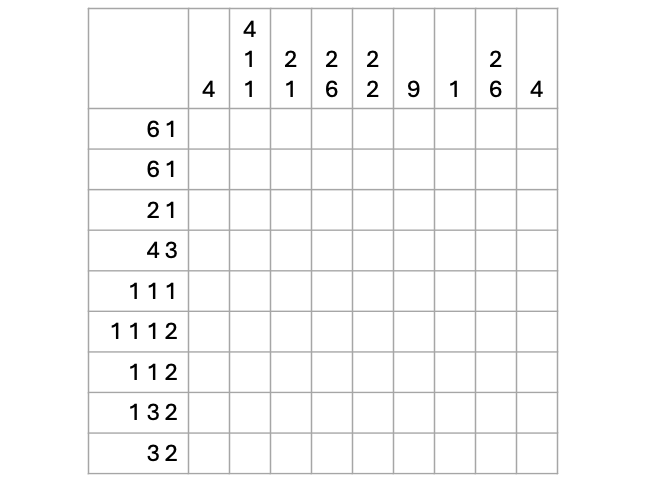
Here is an example of a nonogram puzzle.
The secret to solving a nonogram puzzle is to find places where squares must be filled in. In the previous example with a 9x9 grid, two of the columns has “6 2”. Because the two blocks plus the minimum separator of one square takes up a total of 9 squares, there is only one way to fill in those columns. You can also sometimes deduce squares in rows or columns that are not totally full. For example, the topmost row has a “6”. Regardless of where this block is placed in the row, the middle three rows must be filled. Because there is also a “1”, two more squares to the left must be filled. As deductions are made, mark squares that both must be and cannot be filled.
The previous puzzle can only be filled as follows, revealing a lock code.
When you make a nonogram, it is best to go back and attempt to solve it. It is possible to make a nonogram that does not have a unique solution. I find it is a bit easier to make a solvable nonogram by filling out the background and making the digits the negative space.